前回の1-1では、オームの法則や合成抵抗を勉強しました。
今回は、電線の抵抗についてです。

えっ電線の抵抗も考えなきゃいけないの??
回路を計算する時は、
電気回路の抵抗 >>>>>>>>> 電線の抵抗
電線の抵抗は無視できるほど小さいので、考えなくても良いんです。
しかし!
第二種電気工事士の試験では電線の抵抗を求める問題も出題されますので
勉強していきましょう〜><
電線の抵抗の特徴
さて、いきなりですが問題です!
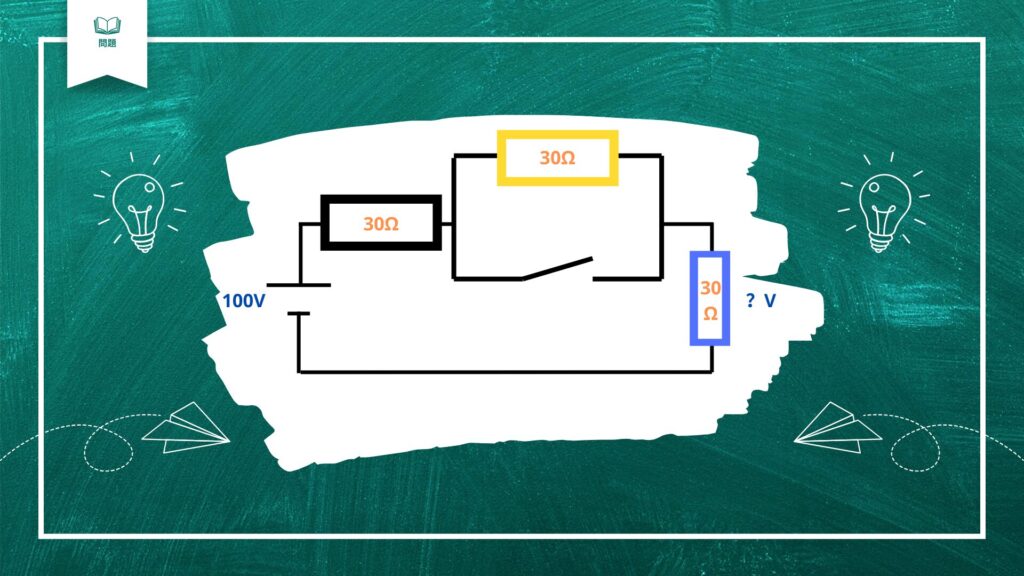
図のような回路でスイッチを閉じた場合
青い抵抗の電圧は何ボルトでしょうか?
この問題を考えるときに重要なのが、
電線の抵抗は黄色い抵抗と比べると無視できるほど小さいということ。
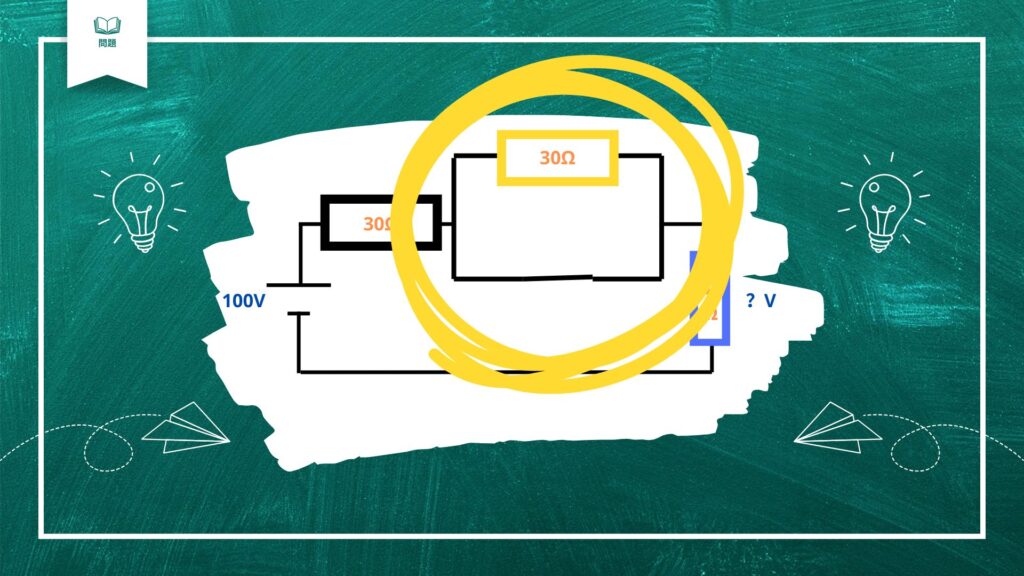
黄色で囲った範囲について考えると
並列回路なので電流は分かれますね。
電流は抵抗が小さいほど流れやすく、抵抗が大きいほど流れにくいのです。
電線の抵抗が黄色い抵抗と比べると無視できるほど小さいので、
ほとんどの電流はスイッチ側を通っていくことになります。
反対に、回路の抵抗を流れる電流は無視できるほど通らないので
回路はこのように書き換えることができます。
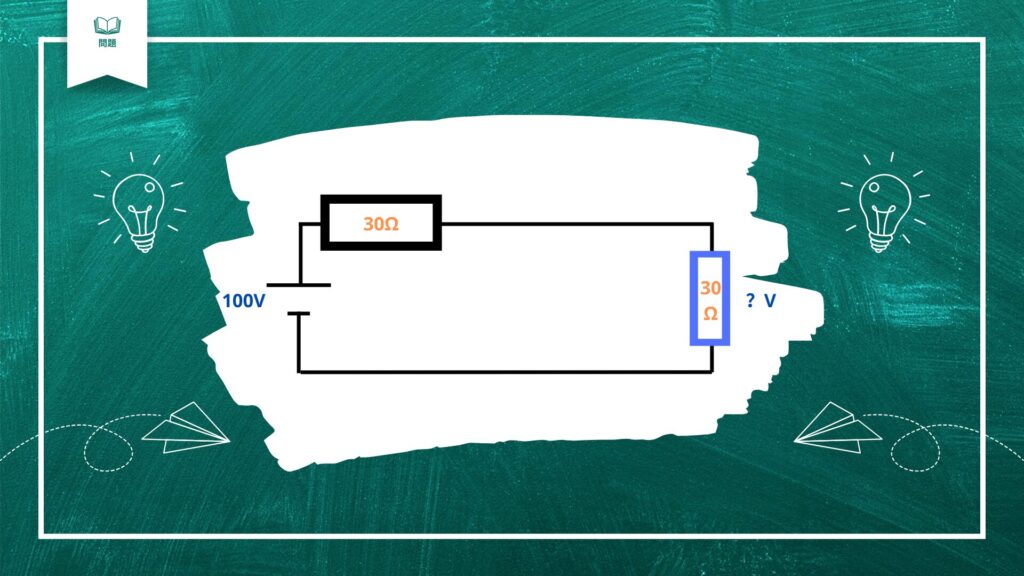
2つの抵抗の直列回路になりました。
ここで、合成抵抗を求めてみましょう。
直列なので、足し算で求めることができます。
30+30=60
合成抵抗は60Ωです。
そうすると、電源の電流を求めることができるようになります。
オームの法則V/RIを使うと
電流I=電圧V/抵抗R
=100/60
=5/3
電源の電流は5/3Aということがわかりました。
直列回路では電流はどこも同じなので、青い抵抗でも電流は5/3Aです。
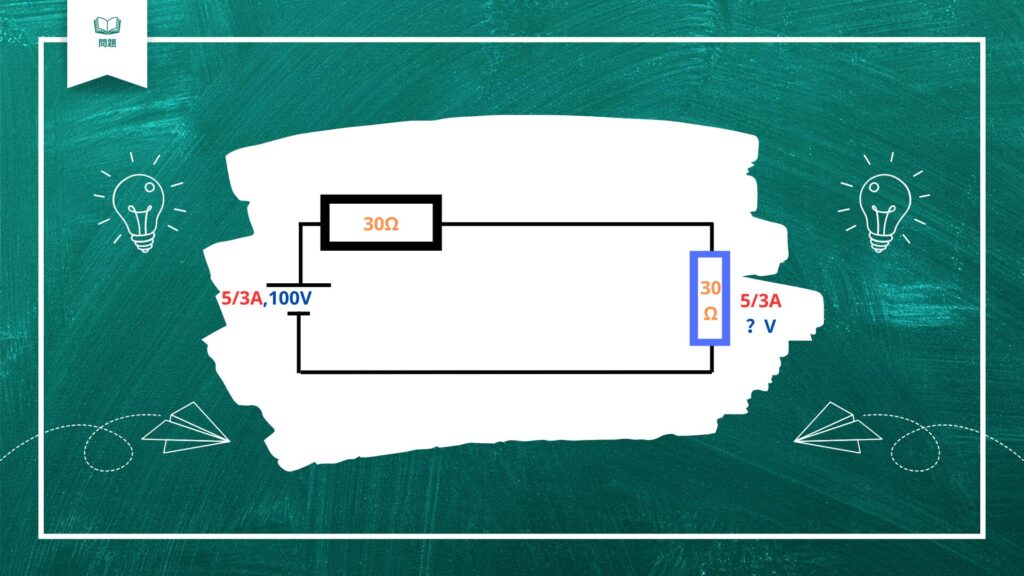
青い抵抗の電流と抵抗がわかったので、
オームの法則V/RIを使って電圧を求めましょう。
電圧V=抵抗R×電流I
=30×5/3
=50
青い抵抗での電圧は、50Vです。
こんな感じで、電線の抵抗の特徴がわかっていれば解ける問題もよく出題されるようです
電線の抵抗の求め方
さて、いよいよ電線の抵抗を計算できるようになりましょう。
公式があるので覚えましょう〜〜((覚えるの嫌だなぁ・・・))

私を含む覚えるのがキライ〜〜な皆さまw
なんとか感覚的に覚えてみる試みです!
よければお付き合いくださいませ^^
電線の抵抗を、自分がトンネルに入る時の抵抗に置き換えてみましょう!

あなたは今歩いています。
歩いていて、先が見えないような距離がながーーーいトンネルがありました。

うわぁっ入りたくない・・!
先が見えないほど長いトンネルはすごく抵抗感があります><
逆に、短いトンネルだとそこまで抵抗を感じることなく通ることができます。
次に、小さいトンネルを見つけました。
かがまないと頭打ちそうやし、水たまりまである〜〜〜

うわぁっ入りたくない・・!(2回目
狭いトンネルは通るのが大変そうだし、入るのに抵抗を感じますね><
逆に、広いトンネルなら通りやすそうです。
そんな感じで、
距離(長さ)が長いほど抵抗が高くなる
広さ(断面積)が狭いほど抵抗が高くなる
ことから、
抵抗=抵抗率×長さ/断面積
という公式をな〜〜んとなく覚えましょうw
試験は4択の選択問題ですし!
ボヤ〜〜っと覚えられていれば大丈夫です!きっと(←
さらに、断面積A=πr2を代入した式もよく出題されています。
半径rよりも直径Dを使った式が多いので、
直径Dを使った式に変換してみましょう。
A=πr2
=π×(D/2)^2
=πD2/4
これを、抵抗の式に代入しましょう。
R=ρL/A
=4ρL/(πD2)
抵抗率ρ〔Ω・m〕、直径D〔mm〕、長さL〔m〕の導線の電気抵抗〔Ω〕を表す式は。
電線の抵抗の式を思い出してみましょう。

こちらですね。
この式の断面積Aに直径Dを代入して解いていくのですが、
直径Dの単位が〔mm〕になっています!

ヤラシー問題だなぁ
1mは100cm、1cmは10mmなので、1mは1000mm=103mmです。
直径D〔mm〕=D×10-3〔m〕と表すことができます。
こちらをA=πr2に代入すると
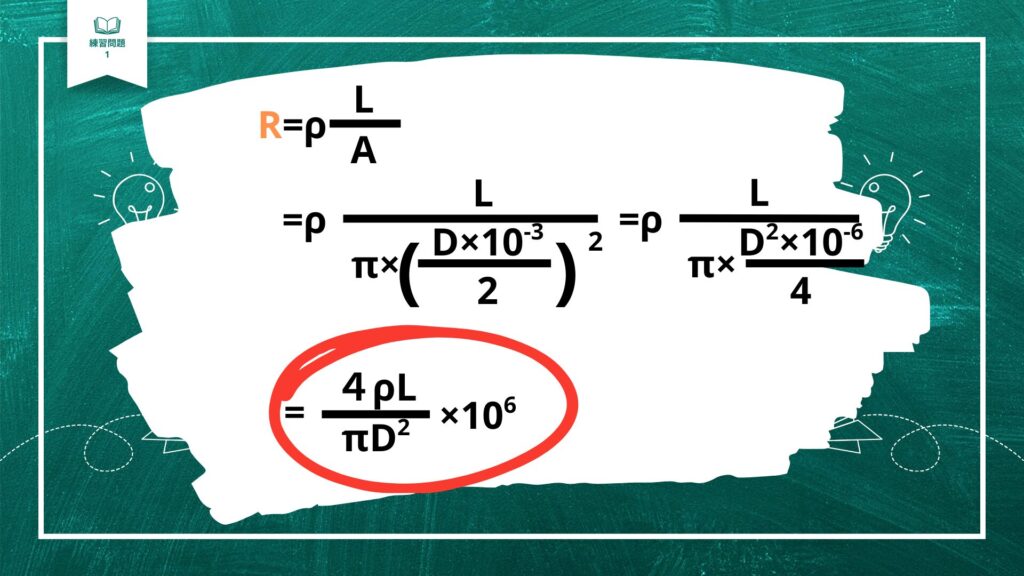
赤で囲った部分が答えになります!
まとめ
お疲れ様でした!
この記事で覚えた内容をおさらいしてみましょう。
電線の抵抗は無視できるほど小さい
電線の抵抗=抵抗率×長さ/断面積
次のページは準備中!
第二種電気工事士まとめページはこちら