オームの法則ってなんやったっけ、、ピオウネです。
皆さんオームの法則って覚えていますか?
私は学校で習った気がするけど・・オームΩって顔文字で使うやつやな〜(・Ω・)
ぐらいしか記憶にございません!笑
ちょっとずつ思い出していきましょう〜_(⌒(_’ω’)ノ
電気回路の基礎は、5〜6問出題されます。
点数で言うと、10〜12点分です。
計算問題が解けるように一緒に頑張りましょう!
こちらの記事はざっと読むだけでもOKです
計算問題の記事でもていねいに解説していきますので、
問題を解きながら理解していきましょ^^
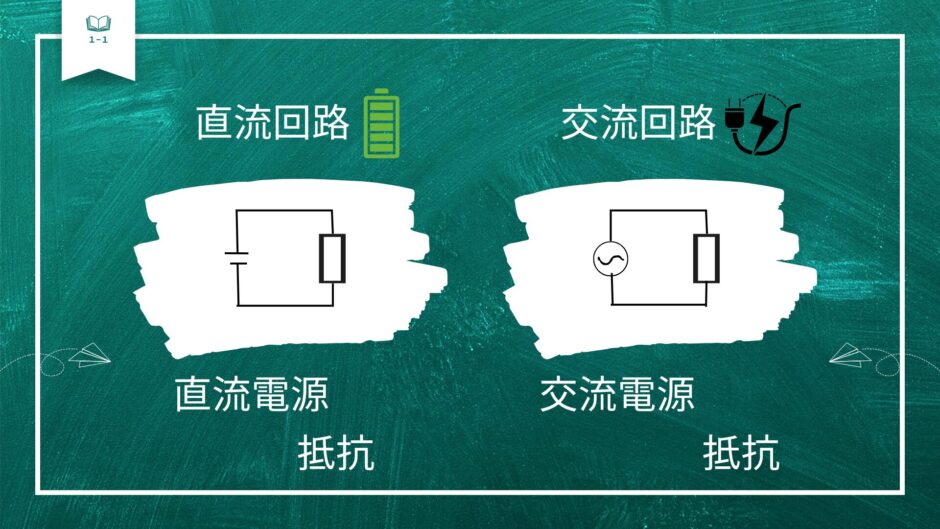
電源の種類(直流電源と交流電源)
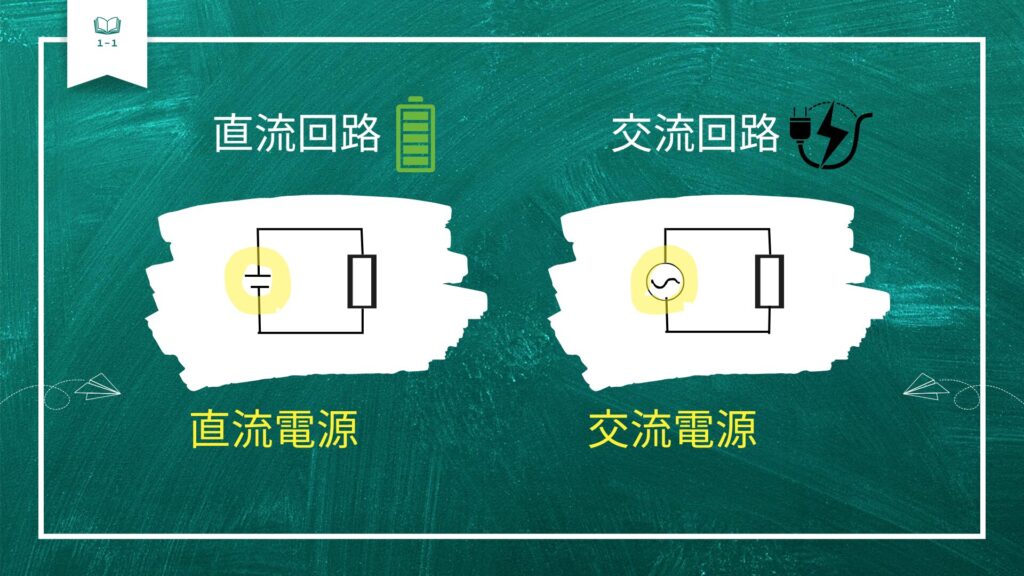
こちらに2つの電気回路があります。
1箇所だけ違うところがありますね。
黄色く囲っているところが電源を表していまして、
左側が直流電源、右側が交流電源を示しています。
直流電源はDCとも呼ばれ、乾電池が該当します。
交流電源はACとも呼ばれ、コンセントが該当します。
電気回路の計算において、直流電源か交流電源かは大きく変わってきます。
しっかり見分けるようにしましょう^^
電圧・抵抗・電流の単位
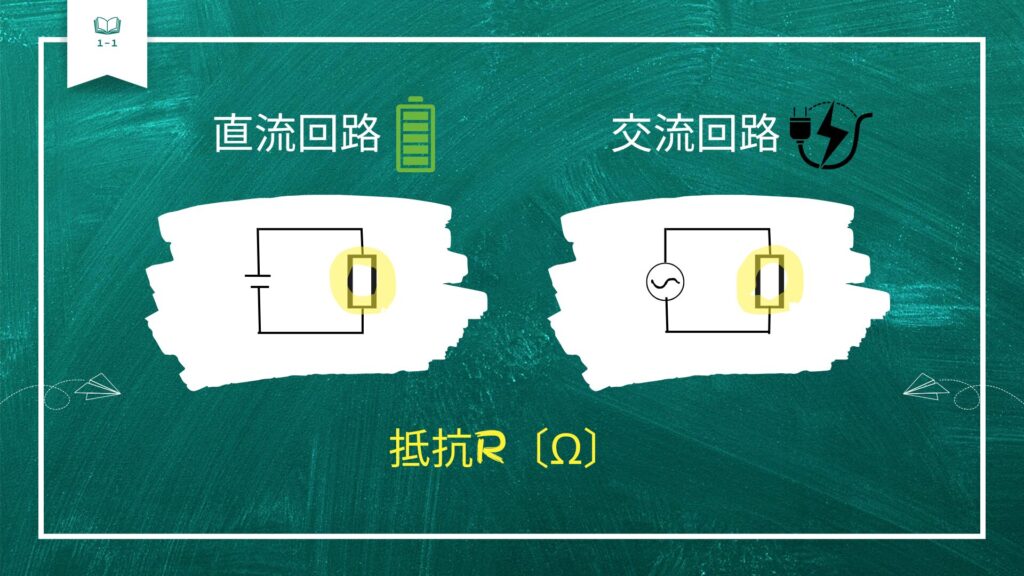
先ほどの電気回路で、電源のほかに四角い記号がありますね。
こちらを抵抗といいます。
抵抗は、電球などが該当します。
電圧Vの単位は〔V(ボルト)〕
抵抗Rの単位は〔Ω(オーム)〕
電流Iの単位は〔A(アンペア)〕
オームの法則 VRIブリで覚えよう!
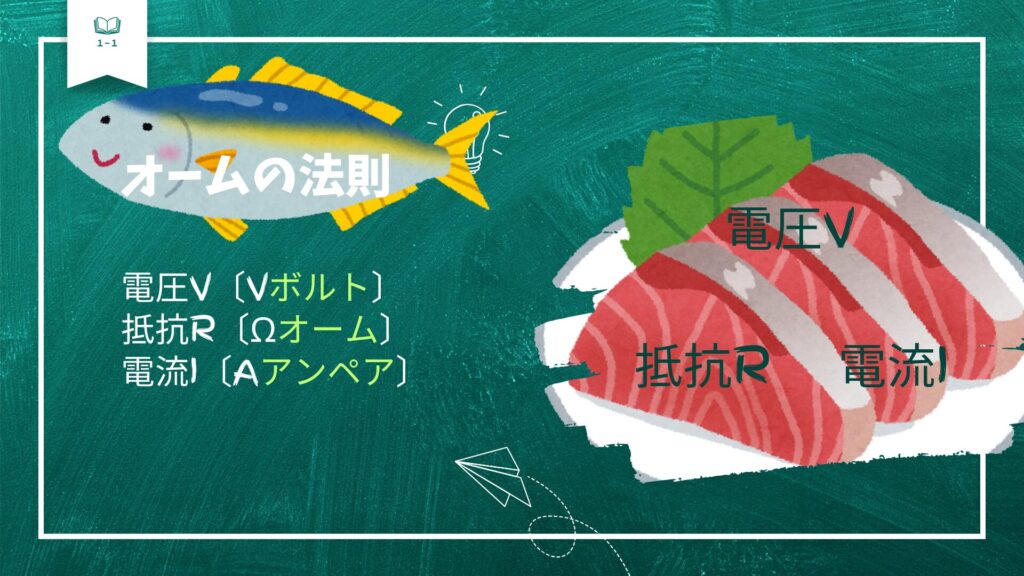
抵抗、電流、電圧を一つの式に表したものがオームの法則です。
V /(R×I)=1 →ブリと覚えましょう!
抵抗R=電圧V/電流I
電流I=電圧V/抵抗R
電圧V=抵抗R×電流I
直列回路と並列回路
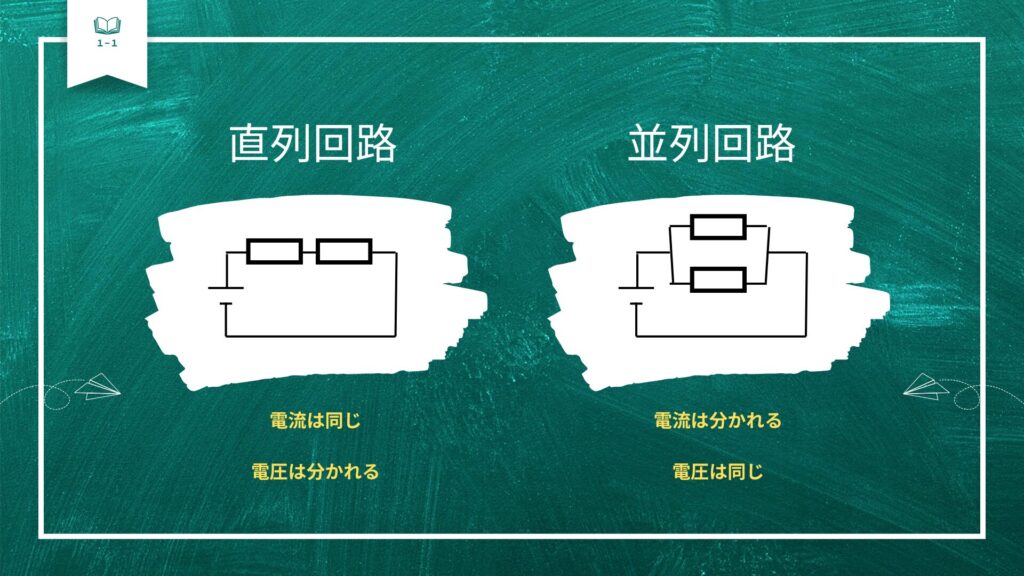
左が直列回路で右が並列回路です。
直列回路は、抵抗が1本の線状にまっすぐ連なっている回路です。
直列回路では、電流はどこも同じ・電圧は分かれるという特徴があります。
並列回路は、回路が分かれていて抵抗が並んでいる回路です。
並列回路では、電流は分かれる・電圧はどこも同じという特徴があります。
この特徴を使って、問題を解いてみましょう!
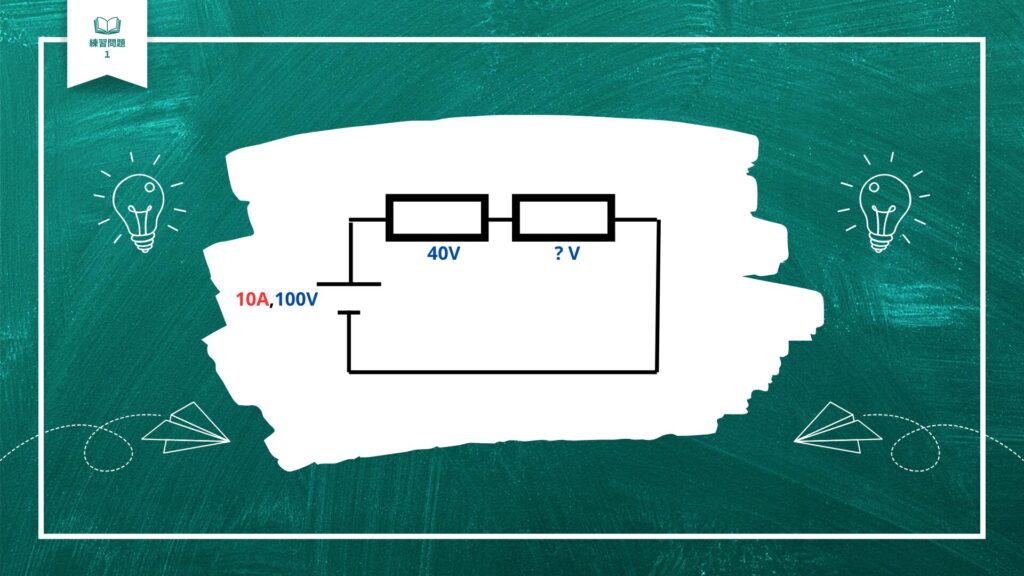
こちらの回路で、右側の抵抗の電圧は何Vでしょうか?
まず、こちらの回路が直列回路と並列回路どちらなのかを考えてみましょう。
これは抵抗が真っ直ぐ連なっているので直列回路ですね。
直列回路の特徴は、電流はどこも同じ・電圧は分かれるでした。
電流はどこも同じなので、左の抵抗でも10A,右の抵抗でも10Aです。
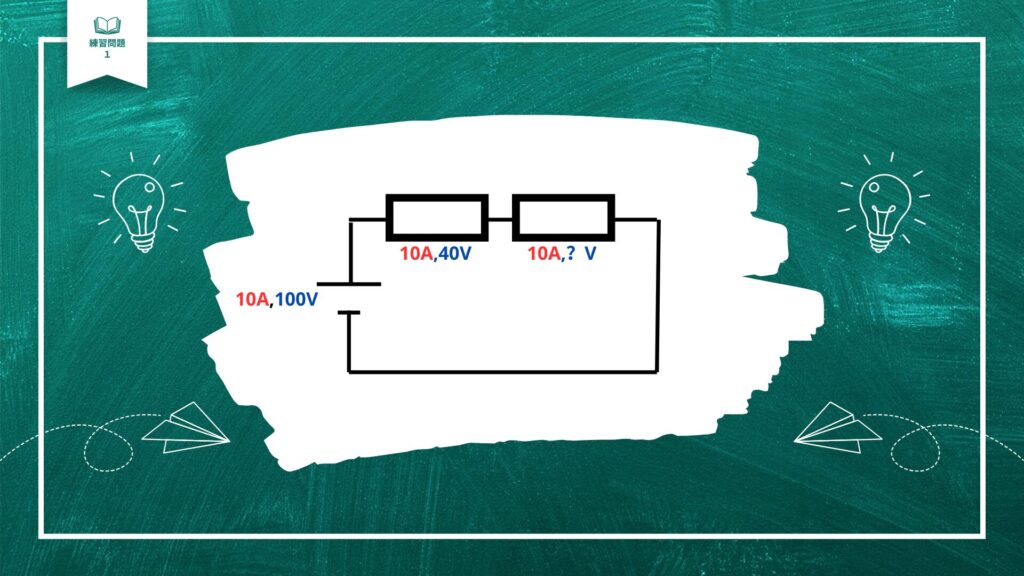
そして、電圧は場所によって分かれます。
今回全体の電圧が100Vなので、
2つの抵抗の電圧を足せば、全体の電圧100Vになります。
左の抵抗が40Vとわかっているので右の抵抗は100-40=60Vとなります。
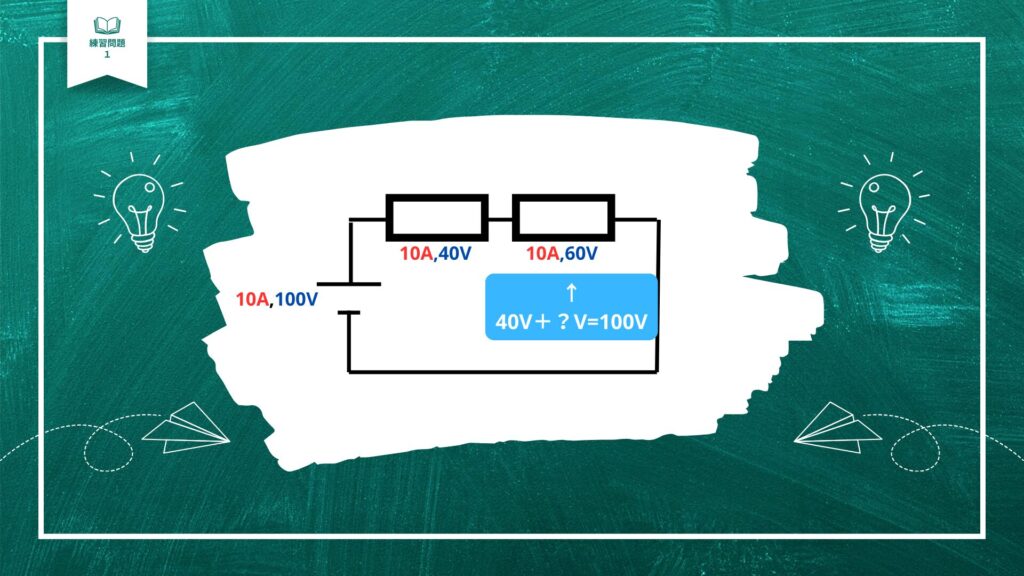
ちなみに、オームの法則を使って抵抗を求めることができます。
ぜひ一緒にやってみましょう。
オームの法則はブリV/RIでしたね。
電圧と電流が分かっていて、抵抗を求めたい場合は、
抵抗R=電圧V/電流Iで求めることができます。
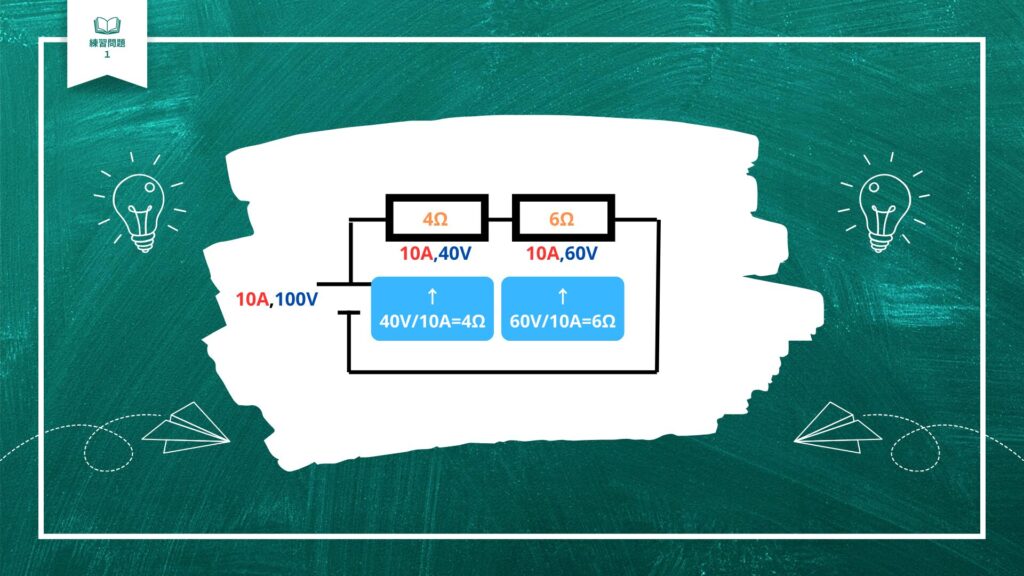
それぞれ、左の抵抗では40V/10A=4Ω 右の抵抗では60V/10A=6Ωです。
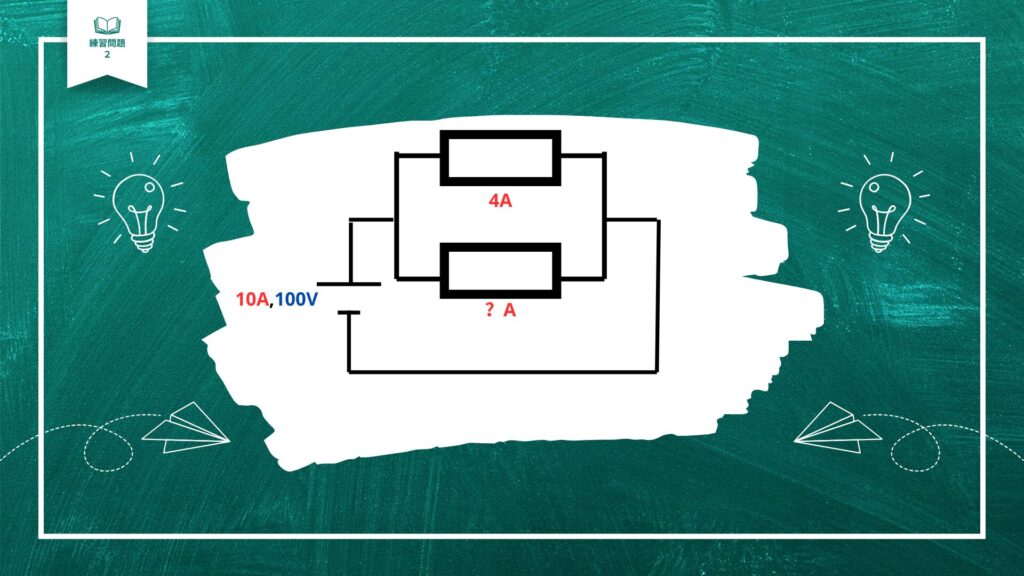
こちらの回路で、下の抵抗の電流は何Aでしょうか?
こちらも直列回路か並列回路かを考えてみましょう。
回路が分かれていて、抵抗が並んでいるので並列回路です。
並列回路の特徴は電流は分かれる・電圧はどこも同じです.
電源の電流は10Aなので、上の抵抗の電流4Aと下の抵抗の電流を足すと10Aになります。
下の抵抗の電流は10-4=6Aで計算することができます。
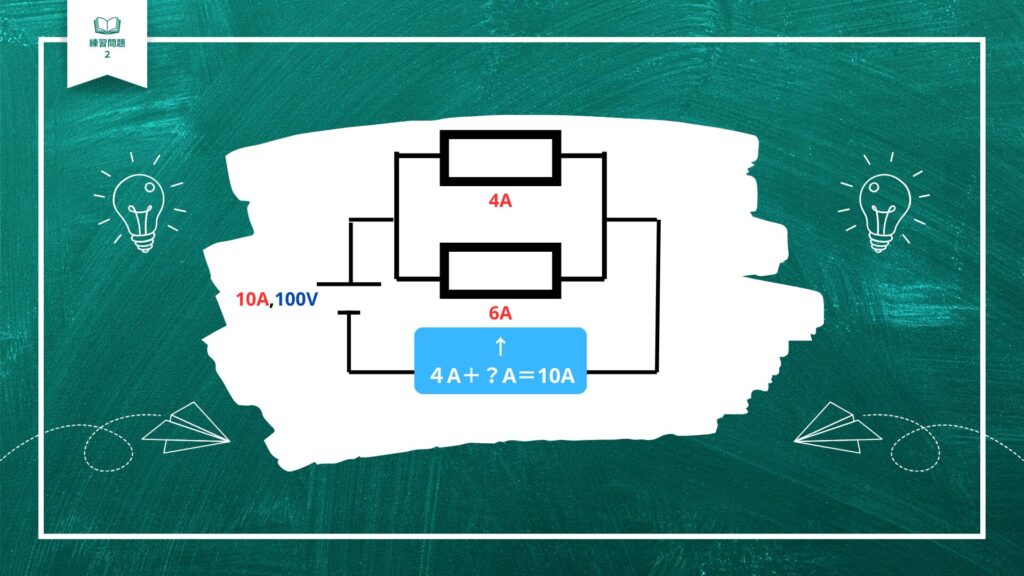
並列回路の特徴は電圧はどこも同じですので、
電圧は上下どちらも電源と同じ100Vですね。
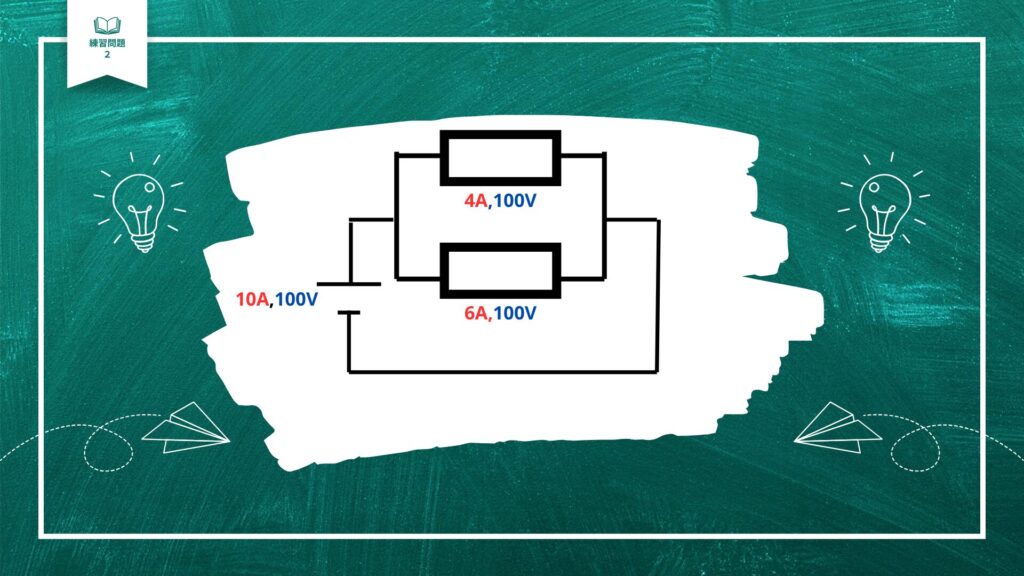
さらに、抵抗も計算してみましょう。
オームの法則はブリV/RIで、抵抗=電圧V/電流Iで計算します。
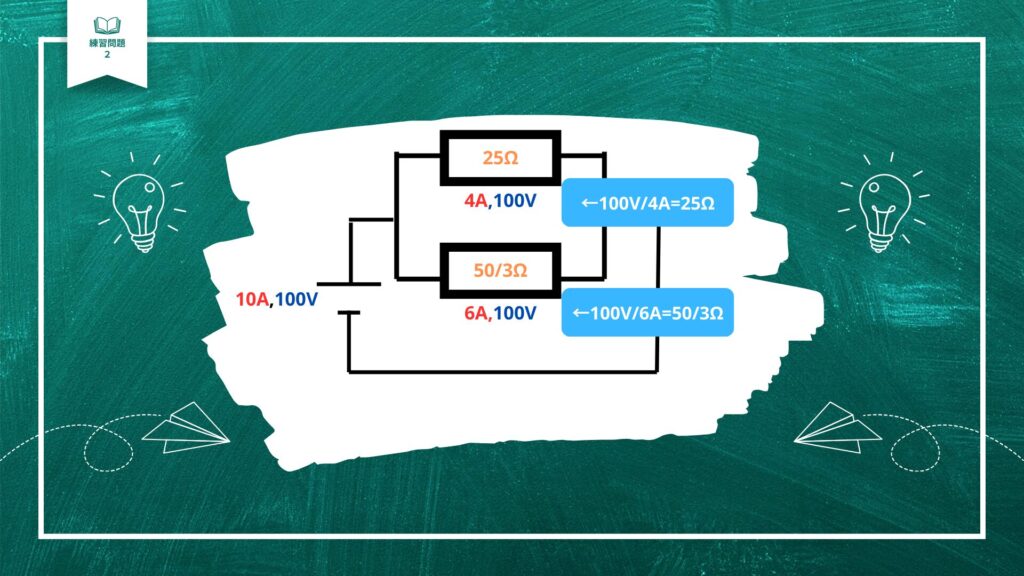
下の抵抗が割り切れない数字ですが・・後ほど説明に使うのでここまでで置いておきます!
合成抵抗
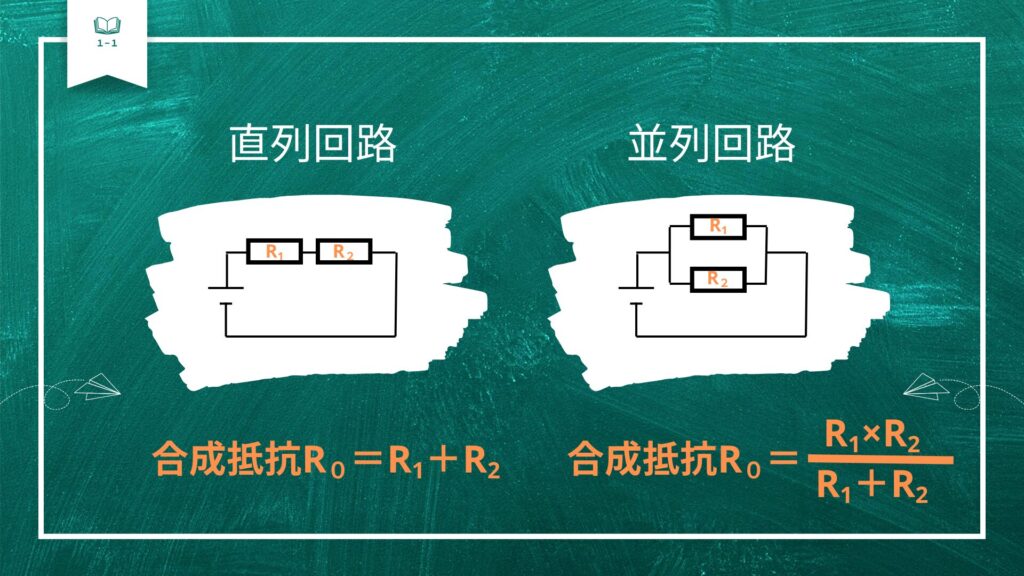
合成抵抗の計算は直列回路と並列回路で求め方が違います。
直列回路は簡単です!足し算すれば合成抵抗になります。
ややこしいのが並列回路で、和(足し算)分の積(掛け算)で覚えましょう。
先ほどの練習問題を使って、実際に計算してみましょう。
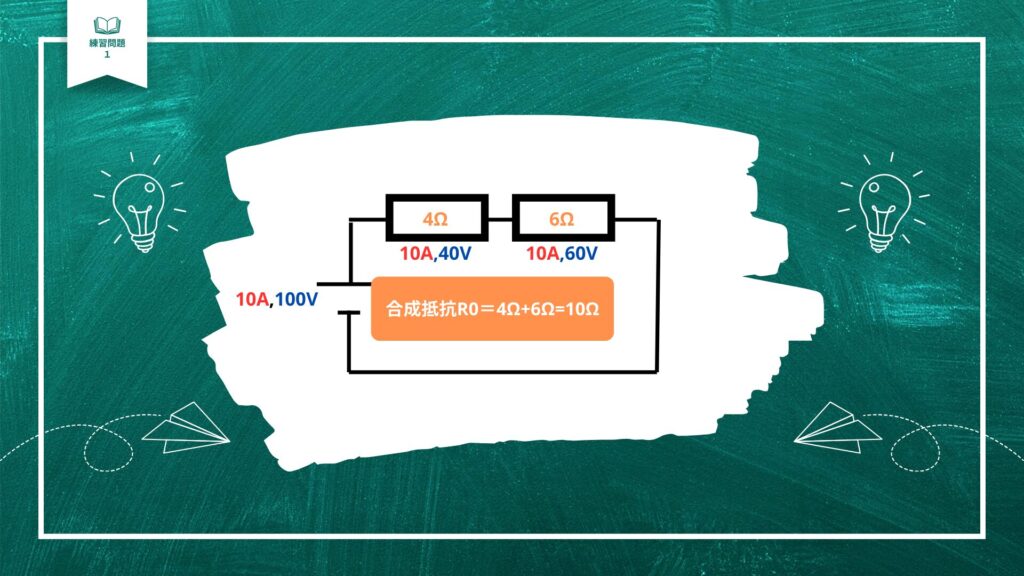
直列回路は、足し算でしたね。
左の抵抗4Ωと右の抵抗6Ωを足して、合成抵抗は10Ωです。
合成抵抗は、電源の電流・電圧とオームの法則が成り立ちます。
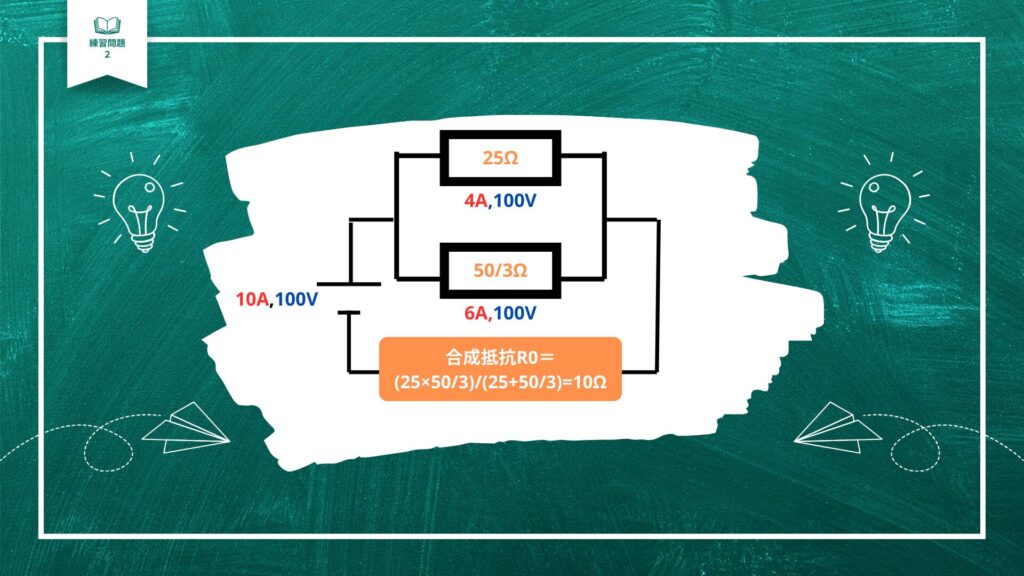
ものすごくわかりづらい式になってしまってごめんなさい・・!
並列回路なので、和分の積で計算します。
計算式は、
(25×50/3)/(25+50/3)
上下どちらも3をかけると、
=(25×50)/(25×3+50)
=(25×50)/(75+50)
=(25×50)/125
どちらも25で割ると、
=50/5
=10
こちらも合成抵抗は10Ωになります。
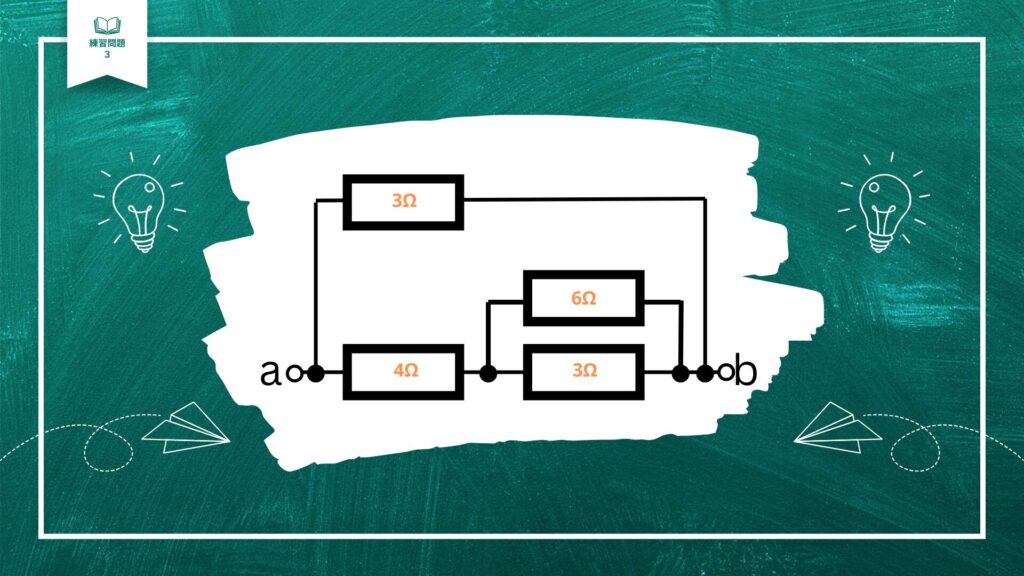
図のような回路で、端子a-b間の合成抵抗〔Ω〕は。
まずは黄色く囲った部分だけの合成抵抗を考えてみましょう。
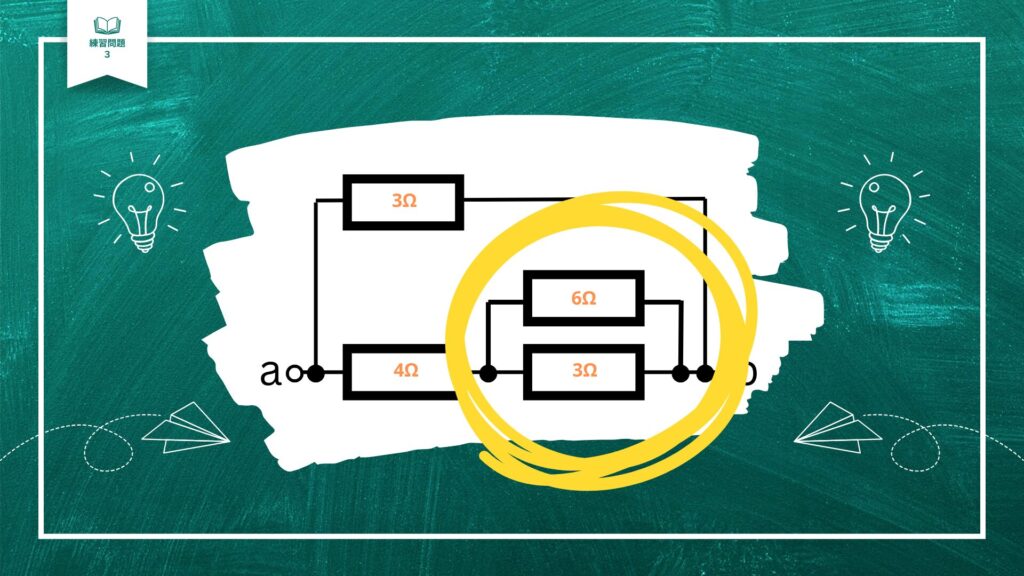
2つの抵抗が並列につながっているので、和分の積で求めてみましょう。
(3×6)/(3+6)
=18/9
=2
黄色い丸で囲った範囲の合成抵抗は、2Ωということがわかりました。
なので、このような回路に書き換えることができます。
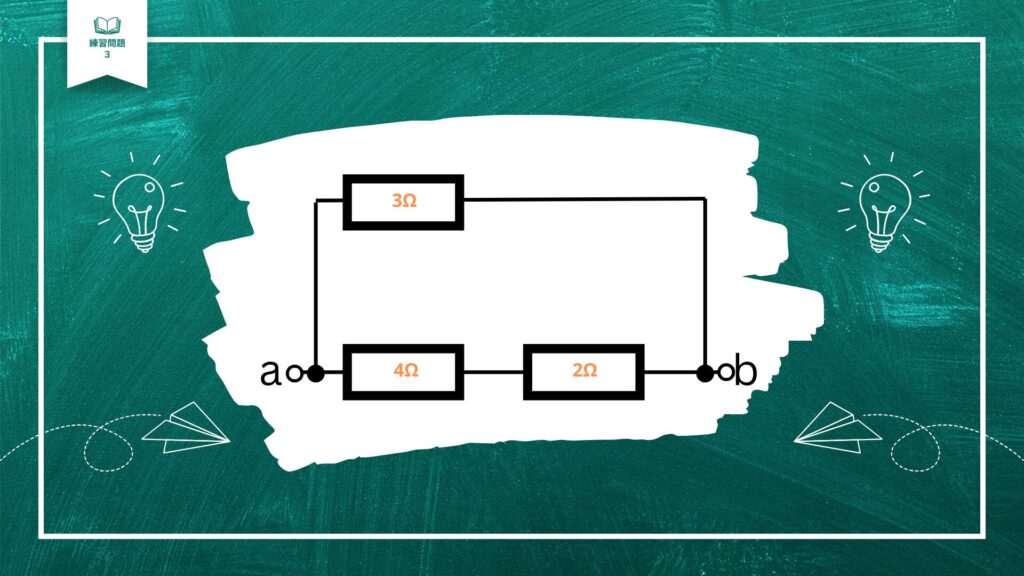
次に、ピンクで囲った範囲の合成抵抗を考えてみましょう。
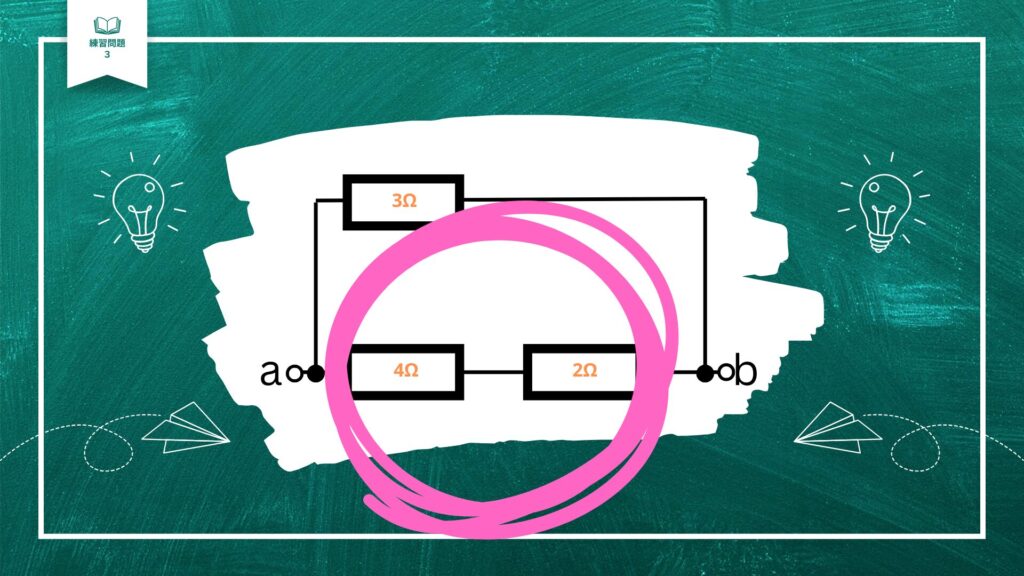
2つの抵抗が真っ直ぐ連なっているので直列ですね。
直列の合成抵抗を足し算で求めることができます。
4+2= 6
ピンクで囲った範囲の合成抵抗は、6Ωということがわかりました。
もう一度回路を書き換えると、
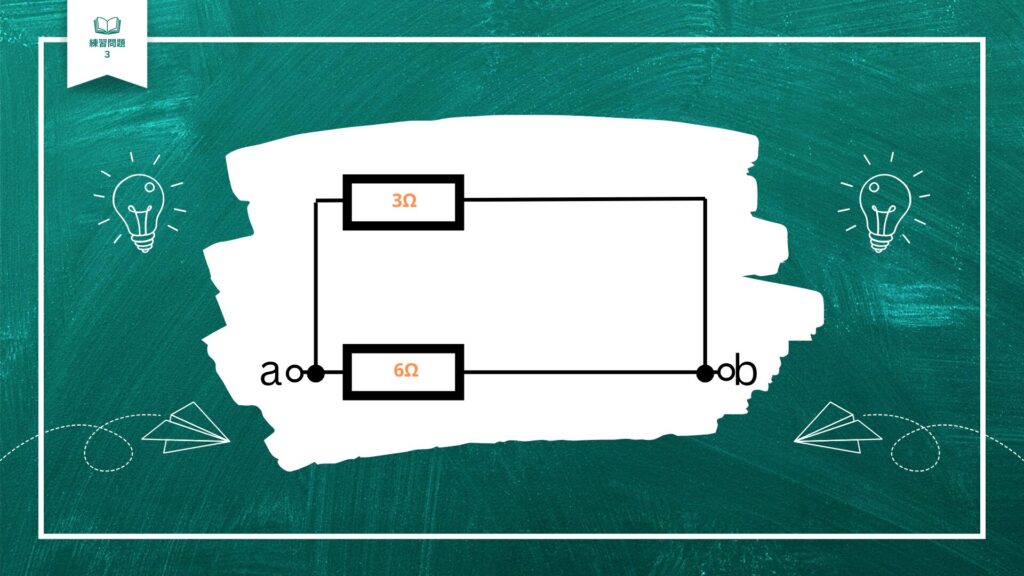
並列につながっているので、和分の積で求めましょう。
(3×6)/(3+6)
=18/9
=2
よって、a-b間の合成抵抗は2Ωです!
まとめ
お疲れ様でした!
この記事で覚えた内容をおさらいしておきましょう。
電圧Vの単位はV(ボルト)
抵抗Rの単位はΩ(オーム)
電流Iの単位はA(アンペア)
この3つの関係は、V/RIブリで覚えましょう🐟
直列回路の合成抵抗は、足し算
並列回路の合成抵抗は、和分の積
次のページはこちら
第二種電気工事士まとめページはこちら